Método de reducción para resolver sistemas de ecuaciones de 2x2 y 3x3

En la resolución de sistemas de ecuaciones se nos presenta un método muy utilizado como lo es el método de reducción.

Método de reducción

El método de reducción es llamado también método de eliminación, consistiendo en la aplicación de operaciones básicas como suma y resta entre las ecuaciones del sistema, de esta manera lograr eliminar una de las variables.

Pasos para la aplicación del método de reducción

Para aplicar este método consideraremos los siguientes pasos:

1.- Ordena las variables de cada ecuación, ubicándolas una debajo de la otra.

2.- Realiza las operaciones básicas entre las ecuaciones hasta eliminar una de las variables.

3.- Del paso anterior, tendrás como resultado una ecuación en función a una sola variable, que debes despejar hasta obtener su valor.

4.- Conocido el valor de una de las incógnitas puedes sustituirlo en cualquiera de la ecuaciones anteriores para conseguir la variable faltante.

Ejemplos de la aplicación del método de reducción

Resolver los siguientes sistemas de ecuaciones aplicando el método de reducción:

1.- $\left\{\begin{matrix} -2x+6y=1& \\ 2x+2y=3& \\ \end{matrix}\right.$

Solución

ordenamos la ecuación y realizamos las operaciones básica;

conocido el valor de Y lo sustituimos en cualquiera de las ecuaciones anteriores para conseguir el valor de X;

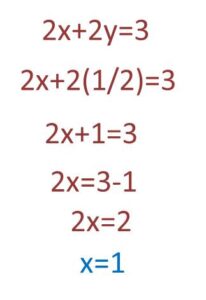
2.- $\left\{\begin{matrix} x+5y=1& \\ 4x+2y=2& \\ \end{matrix}\right.$

Solución

a simple vista no se puede eliminar ninguna de las variables, por tanto es necesario multiplicar una de las ecuaciones por un valor que permita eliminar una incógnita, veamos;

$x+5y=1$

$-4.(x+5y=1.(-4))$

$(-4x-20y=-4)$

sustituimos la ecuación en el sistema;

$\left\{\begin{matrix} -4x-20y=-4& \\ 4x+2y=2& \\ \end{matrix}\right.$

procedemos a reducir la ecuación;

3.- $\left\{\begin{matrix} x-y+z=3 & & \\ x+2y+z=4 & & \\ x-y-2z=5& & \\ \end{matrix}\right.$

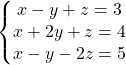
Solución

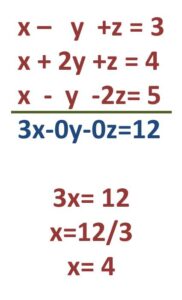
conociendo el valor de X lo sustituimos en la ecuación uno y tres, para trabajar con un sistema de ecuaciones 2×2, de esta forma eliminar una de las variables;

conociendo el valor de X y de Z, sustituimos en cualquier ecuación para conseguir el valor de Y;

x-y+z=3

4-y+(-2/3)=3

-y=3-4+2/3

-y=-1+2/3

y=1/3