Regla de Cramer con ejercicios resueltos paso a paso

Resolver sistemas de ecuaciones es una tarea fundamental en álgebra lineal y una de las técnicas más utilizadas es el método de Cramer. Si alguna vez te has preguntado qué es la regla de Cramer, cómo funciona y cuándo aplicarla, en esta publicación te lo explicaré paso a paso con ejemplos prácticos.

Contenido

Regla de Cramer

La regla de Cramer es una expresión algebraica en términos de determinantes, para la búsqueda de las soluciones de un sistema de ecuaciones lineales con tantas ecuaciones como incógnitas, siempre y cuando el sistema tenga una solución única.

Consideraciones de la Regla de Cramer

Dentro de las consideraciones para su aplicación se encuentran:

1.- El número de ecuaciones debe ser igual al número de incógnitas, es decir, la matriz debe ser cuadrada.

2.- El determinante de la matriz de los coeficientes deber ser distinto a cero.

La regla de Cramer es practico en la resolución de sistemas de ecuaciones 2×2 y sistema de ecuaciones 3×3, siendo bastante engorrosos con sistemas de mayores ecuaciones e incógnitas, pero sigue siendo aplicable.

Aplicación de la regla de Cramer

Para aplicar esta regla, es necesario hallar la matriz ampliada, la cual está asociada al sistema de ecuaciones, donde la primera columna estará formada por los coeficientes de la primera incógnita de las ecuaciones.

Por ejemplo si tenemos un sistema de ecuaciones 2×2 la expresión matricial quedaría;

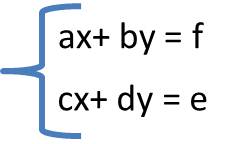
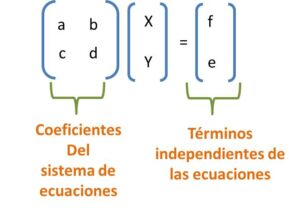
donde X y Y son las variable, resaltando que dependiendo del numero de ecuaciones e incógnita la expresión se agranda.

Luego de realizado esto, podemos proceder a calcular el determinante de la primera matriz, cuyo resultado dividirá los resultados de tres determinante posteriores, correspondientes al calculo de las incógnitas x,y ó z según sea el caso.

Es aquí, en este procedimiento que aplicamos la denominada regla de Cramer, consistiendo en ir sustituyendo la primera columna de la determinante inicial por los términos independientes, dividida por el resultado antes obtenido, de esta forma conseguir el valor de X. El procedimiento se repite para las otras variables cambiando el valor de las columna dos y/0 tres respectivamente.

La formula general para un sistema de ecuaciones 2×2 sería:

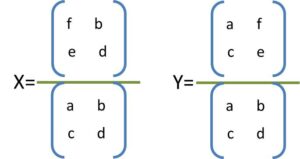
Cómo resolver un sistema de ecuaciones con el método de Cramer

Para resolver un sistema de ecuaciones con este método, sigue los siguientes pasos:

Paso 1: Representar el sistema en forma de matrices

Dado el sistema de ecuaciones:

$\begin{aligned} ax + by &= c \\ dx + ey &= f \end{aligned}$

Se representa como:

$A \cdot X = B$

con:

$A = \begin{bmatrix} a & b \\ d & e \end{bmatrix}, \quad X = \begin{bmatrix} x \\ y \end{bmatrix}, \quad B = \begin{bmatrix} c \\ f \end{bmatrix}$

Paso 2: Calcular el determinante de la matriz de coeficientes $D$

Se calcula como:

$D = \begin{vmatrix} a & b \\ d & e \end{vmatrix} = (a \cdot e) - (b \cdot d)$

Si $D = 0$ , el sistema no tiene solución única.

Paso 3: Calcular los determinantes $D_x$ y $D_y$

Sustituimos la columna de los coeficientes de $x$ y $y$ por la columna de términos independientes:

$D_x = \begin{vmatrix} c & b \\ f & e \end{vmatrix}, \quad D_y = \begin{vmatrix} a & c \\ d & f \end{vmatrix}$

Se calculan de la misma forma que $D$ .

Paso 4: Obtener los valores de $x$ y $y$

Usamos la fórmula:

$x = \frac{D_x}{D}, \quad y = \frac{D_y}{D}$

Ejemplo de la Regla de Cramer

Ejercicio 1: Resolver el siguiente sistema de ecuaciones aplicando la regla de Cramer:

$\left\{\begin{matrix} 4x&+5y=2 \\ x&-3y=4 \\ \end{matrix}\right.$

Solución

construimos la matriz;

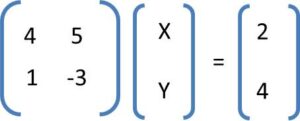
calculamos el determinante;

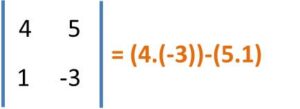
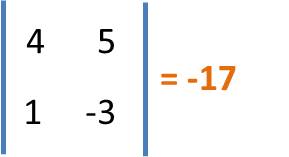
calculamos el valor de (x) y (y);

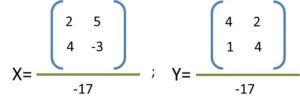
donde;

$x=\frac{26}{17}$

$y=\frac{14}{-17}$

Ejercicio 2: Resolvamos el siguiente sistema:

$\left\{\begin{matrix} 2x& + 3y = 5 \\ 4x& - y = 1 \\ \end{matrix}\right.$

Solución

Paso 1: Escribir la forma matricial del sistema
Un sistema de la forma:

$ax + by = c$

$dx + ey = f$

se puede escribir en forma de matrices como:

$A \cdot X = B$

donde:

$A = \begin{bmatrix} 2 & 3 \\ 4 & -1 \end{bmatrix}$

$X = \begin{bmatrix} x \\ y \end{bmatrix}$

$B = \begin{bmatrix} 5 \\ 1 \end{bmatrix}$

Paso 2: Calcular el determinante de la matriz de coeficientes $A$

$D = \begin{vmatrix} 2 & 3 \\ 4 & -1 \end{vmatrix}$

Se calcula como:

$D = (2 \cdot (-1)) - (3 \cdot 4) = -2 - 12 = -14$

Paso 3: Calcular $D_x$
Se forma reemplazando la primera columna de $A$ por la columna de términos independientes $B$ :

$D_x = \begin{vmatrix} 5 & 3 \\ 1 & -1 \end{vmatrix}$

$D_x = (5 \cdot (-1)) - (3 \cdot 1) = -5 - 3 = -8$

Paso 4: Calcular $D_y$
Se forma reemplazando la segunda columna de $A$ por la columna de términos independientes $B$ :

$D_y = \begin{vmatrix} 2 & 5 \\ 4 & 1 \end{vmatrix}$

$D_y = (2 \cdot 1) - (5 \cdot 4) = 2 - 20 = -18$

Paso 5: Calcular $x$ y $y$

$x = \frac{D_x}{D} = \frac{-8}{-14} = \frac{4}{7}$

$y = \frac{D_y}{D} = \frac{-18}{-14} = \frac{9}{7}$

Solución

$x = \frac{4}{7}, \quad y = \frac{9}{7}$

Ejercicio 3. Resolvamos el siguiente sistema:

$\left\{\begin{matrix} 3&x - 2y = 7 \\ 5&x + 4y = -3\\ \end{matrix}\right.$

Solución

Paso 1: Escribir la forma matricial del sistema

$A = \begin{bmatrix} 3 & -2 \\ 5 & 4 \end{bmatrix}$

$B = \begin{bmatrix} 7 \\ -3 \end{bmatrix}$

Paso 2: Calcular el determinante de $A$

$D = \begin{vmatrix} 3 & -2 \\ 5 & 4 \end{vmatrix}$

$D = (3 \cdot 4) - (-2 \cdot 5) = 12 + 10 = 22$

Paso 3: Calcular $D_x$

$D_x = \begin{vmatrix} 7 & -2 \\ -3 & 4 \end{vmatrix}$

$D_x = (7 \cdot 4) - (-2 \cdot -3) = 28 - 6 = 22$

Paso 4: Calcular $D_y$

$D_y = \begin{vmatrix} 3 & 7 \\ 5 & -3 \end{vmatrix}$

$D_y = (3 \cdot -3) - (7 \cdot 5) = -9 - 35 = -44$

Paso 5: Calcular $x$ y $y$

$x = \frac{D_x}{D} = \frac{22}{22} = 1$

$y = \frac{D_y}{D} = \frac{-44}{22} = -2$

Solución

$x = 1, \quad y = -2$

Te recomendamos revisar la pagina de sistemas de ecuaciones 3×3 donde se presenta la resolución de un sistema a partir de la regla de Cramer.