Los sistemas de ecuaciones son un conjunto de dos o mas ecuaciones con dos o mas incógnitas, que según el números de estas se pueden clasificar en sistemas ecuaciones 2×2 ó sistemas de ecuaciones 3×3.
Contenido
Sistemas de ecuaciones 2×2
Los sistemas de ecuaciones 2×2, están conformadas por dos ecuaciones con dos incógnitas, por ejemplo:
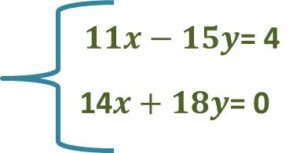
Métodos de resolución de un sistema de ecuaciones 2×2
Dentro de los métodos mas utilizados de resolución de un sistema ecuaciones 2×2 se encuentra:
.- Método de eliminación o reducción.
.- Método de igualación .
.- Método de sustitución.
Ejercicios de sistemas de ecuaciones 2×2
Resolver los siguientes sistemas de ecuaciones:
1.-![]()
Solución
aplicaremos en método de reducción ó eliminación, es decir, verificamos que este ordenadas las variables en cada ecuación realizando la sumas o restas según el caso;
![]()
![Rendered by QuickLaTeX.com \[\frac{\left\{\begin{matrix} 2x+4y=2 & \\ 3x-4y=1 & \\ \end{matrix}\right.}{5x=3}\]](https://ecuaciones20.com/wp-content/ql-cache/quicklatex.com-4e816af171fc9a734e3b379d8328eb7e_l3.png)
despejamos de la ecuación la variable x;
![]()
![]()
sustituimos este valor en cualquiera de las dos ecuaciones para conseguir el valor de (y);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
la solución al sistema de ecuaciones es ![]() y
y ![]()
2.-![]()
Solución
para este ejercicios aplicaremos el método de sustitución, tomaremos una ecuación y despejamos una variable;
![]()
![]()
sustituimos en la otra ecuación
![]()
![]()
despejamos la variable;
![]()
![]()
![]()
![]()
conocido el valor de (y) lo sustituimos en la primera ecuación donde se despejo la variable x;
![]()
![]()
![]()
la solución al sistema de ecuaciones es ![]() y
y ![]()
3.-![]()
Solución
utilizaremos el método de igualación, para ello despejamos la misma variable de cada ecuación;
![]()
![]()
![]()
![]()
![]()
igualamos las ecuaciones y agrupamos términos;
![]()
![]()
![]()
![]()
![]()
conocido el valor de (y) sustituimos en cualquiera de las ecuaciones despejadas al inicio para conseguir el valor de (x);
![]()
![]()
![]()
![]()
la solución para el sistema de ecuaciones es ![]() y
y ![]()
